X-algorithm (feat. Dancing Link)

1. 개요

X 알고리즘은 전설적인 컴퓨터공학자이자 수학자인 Knuth에 의해 Dancing Link를 소개하면서 같이 서술한 알고리즘으로  Exact Cover 문제를 좀 더 효과적으로 해결하고자 만들어진 알고리즘이다. 이때, 여타 기법들과 동일하게 Back Tracking 기법을 사용하는 알고리즘이지만 Back Tracking을 적용하는 대상에 차이가 있다는 특징이 있다. 일반적인 Back Tracking 알고리즘의 경우에는 직접 시도하며 제약조건을 만족하는지를 판단하고 다시 뒤로 돌아오는 전략을 취하지만, X 알고리즘의 경우에는 각 제약조건들을 열로 잡고 행은 가능한 경우를 넣은 0-1 행렬 내에서 Back Tracking을 진행한다.

2. 방법

X 알고리즘은 처음 보면 이해하기 상당히 까다롭다. 행과 열이 어떤 의미를 갖고 있는지에 대해 명확히 서술하지 않기 때문이다. 이에 대해 좀 더 설명해 보면, N-queen 문제와 같이 같은 열에는 하나의 여왕만 존재해야 한다, 같은 행에는 하나의 여왕만 존재해야 한다, 같은 대각선에는 하나의 여왕만 존재해야 한다와 같은 제약 조건을 column으로 잡고, 여왕이 배치될 수 있는 모든 경우를 각각의 행으로 잡는다. 이때, 여왕이 배치되는 경우에 따라 만족되는 제약조건이 있으면 해당 위치를 1로 잡고 아니라면 0으로 잡은 행렬이 구성된다. 논문에서는 이 행렬을 순환 구조를 가진 이중 연결 리스트들로 구성하여 만약 0 이면 노드가 존재하지 않고 1인 경우에만 해당 row와 column에 위치하는 노드가 있도록 하였다.

 

알고리즘 자체는 간단하다. 제약 조건을 만족시키는 행이 있는 경우, 그 열을 일시적으로 행렬에서 제거하고, 이 열에서 1을 가지는 행도 같이 제거한다. 이 과정을 행렬이 남아있을 때까지 반복하는 것을 통해서 겹치지 않고 전체의 제약 조건을 만족시키는 exact cover를 구할 수 있다. 만약, 반복을 진행했을 때, 없어지지 않고 남아있는 열이 존재한다면 알고리즘이 실패한 것이므로 다시 돌아가서 다른 열을 선택하며 진행된다.

 

이에 대해 좀 더 명확하게 서술하면

A 가 0과 1로 이루어진 행렬인 경우,

1. 만약 A 가 비어있는 경우, 해결된 것이기에 종료한다.
2. 비어있지 않다면, A의 열 c를 비결정론적으로 선택한다.(1의 개수가 가장 적은 열을 선택할 때, 가장 적은 분기가 발생한다.)
3. A의 행 r을 A[r][c] == 1이 되는 지점으로 선택한다.(비결정론적으로)
4. r을 부분해에 넣는다.
5. A[r][j] == 1인 j에 대해 반복한다.
   1. A에서 열 j를 제거한다.
   2. A[i][j] == 1인 i에 대해 반복한다.
      1. A에서 행 i를 제거한다.
6. 1번 과정으로 돌아간다.

위 과정은 X 알고리즘이 수행되는 과정에 대해서 서술된 것이다. 이때, 3번 과정을 보면 비결정론적으로 행을 선택하는 내용이 존재한다. 이는 이 과정에서 row를 선택하는 과정에 따라 다른 결과가 나온다는 것이며, 분기가 발생한다는 것이기에 이 지점에서 재귀적으로 구현이 가능하다는 것을 확인할 수 있다.

이때, knuth는 행과 열을 제거하는 과정을 Cover, 다시 복구하는 과정을 UnCover로 명명했는데. 이는 하나의 경우(row)가 제약조건  (column)을 만족시키는 영역을  탐색에서 제외하기에 Cover로 한 것으로 보이고, UnCover의 경우는 이 Cover의 영역을 다시 탐색영역에 포함하는 과정이기에  UnCover로 명명한 것으로 보인다.

 Cover / Uncover은 Dancing link 방식으로 구현되었으며, Dancing Link의 추가적인 내용은 아래 포스트에서 확인할 수 있다.

Dancing Link

Cover와 Uncover의 과정을 좀 더 자세히 살펴보자면 먼저 Knuth가 어떤 방식으로 matrix A를 구성했는지부터 볼 필요가 있다.

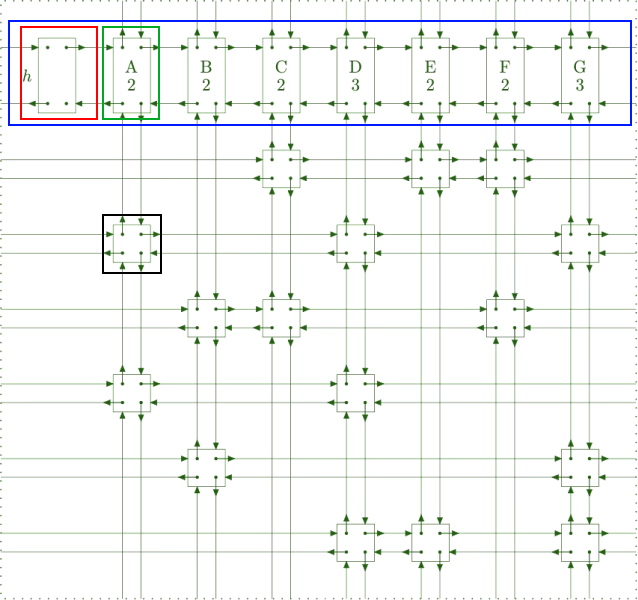
algorithm X 논문에서 사용된 이미지를 사용했다. 하나하나의 부분에 대해 설명하자면, 먼저 빨간색 영역은 master header라고 하며, 각 제약조건(초록색 영역)의 시작이 되는 부분이다. 이때, 제약조건 리스트는 원형 이중 연결리스트로 이루어져 있다.

두번째로 볼 부분은 제약조건(column)에 해당하는 초록색 영역으로 header 라고도 한다. 이 부분은 master와 연결된 형태의 원형 이중연결 리스트를 구성하며, 아래쪽으로는 경우(검은색 영역)와 원형 이중연결 리스트를 구성하는 것을 볼 수 있다.

파란색 영역은 master header와 column으로 이루어진 header list이며, 위에서 언급된 것처럼 원형 이중연결리스트를 구성하고 있다.

마지막으로 검은색 영역은 각 경우에 해당하며, 중간중간 비어있는 부분을 볼 수 있는데 검은색 영역과 같은 형태의 노드가 연결되어있는 경우에는 1로 취급되며 아닌 경우에는 0으로 취급되어 0-1 행렬을 구성하게 된다.

이때, 각 영역의 구성 요소는 다음과 같다.

• 빨간색 영역: 
  1. 왼쪽의 column을 지시하는 변수
  2. 오른쪽의 column을 지시하는 변수
• 초록색 영역:
  1. 왼쪽의 column을 지시하는 변수
  2. 오른쪽의 column을 지시하는 변수
  3. 위(가장 아래쪽)의 row를 지시하는 변수
  4. 아래의 row를 지시하는 변수
  5. 아래쪽 영역에 속한 노드의 수를 담는 변수
• 검은색 영역:
  
  1. 왼쪽의 column을 지시하는 변수
  2. 오른쪽의 column을 지시하는 변수
  3. 위의 노드를 지시하는 변수
  4. 아래의 노드를 지시하는 변수
  5. 경우를 나타내는 변수
  6. column을 지시하는 변수(header list에 존재하는 node를 지시)

이때, 각 노드(n)에 대해 다음과 같은 연산을 진행할 수 있다. L[n](왼쪽 노드), R[n](오른쪽 노드), U[n](위쪽 노드), D[n](아래쪽 노드), C[n](해당 노드가 속한 header), S[n](해당 열의 노드의 수)

 

다음으로 Cover는 0-1행렬에서 해당하는 열을 제거하고 열에 포함된(1을 갖는) row를 제거하는 과정으로 이를 순서대로 표현하면 다음과 같다.

c가 cover의 대상인 열일 때,

1. c를 header list에서 제거한다. (L[R[c]] <- L[c], R[L[c]] <- R[c])
2. i = D[c] 에 대해 아래로 내려가면서 i == c 일 때까지 반복한다.
   1. j = R[i] 에 대해 오른쪽으로 이동하면서 j == i 일 때까지 반복한다.
      1. 위 노드와 아래 노드의 연결을 제거한다.(U[D[j]] <- U[j], D[U[j]] <- D[j])
      2. 해당 노드가 속한 열의 노드의 수를 -1 한다.(S[C[j] <- S[C[j]]] - 1)

Uncover의 경우는 cover에서 제거했던 Column과 row를 복구하는 과정으로 이 과정에서 Dancing Link 기법을 활용하여 빠르게 삭제된 행렬의 부분을 재건한다, 이를 순서대로 표현하면 다음과 같다.

c가 uncover의 대상인 열일 때,

1. i = U[c] 에 대해 위쪽으로 이동하면서 i == c 일 때까지 반복한다.
   1. j = L[i]에 대해 왼쪽으로 이동하면서 j == i일 때까지 반복한다.
      1. 해당 노드가 속한 열의 노드의 수를 +1 한다.(S[C[j]] <- S[C[j]] + 1)
      2. 위 노드와 아래 노드의 연결을 재건한다.(U[D[j]] <- j, D[U[j]] <- j)
2. c를 header list에 재건한다.(L[R[c]] <- c, R[L[c]] <- c)

위에 정리된 내용들을 토대로 알고리즘을 서술하면

h 가 master header이고 k = 0 일 때,

1. R[h] = h 이면 현재까지의 결과를 출력하고 종료한다.
2. 아닌 경우 열 c를 선택한다.(분기가 최소가 되도록, 1인 행의 수가 가장 적은 열을 선택)
3. c 를 cover한다.
4. r = D[c]에 대해 r == c가 될 때까지 아래로 진행한다.
   1. 부분 해 O[k]에 r을 삽입한다.
   2. j = R[r]에 대해 j ==r 이될 때까지 오른쪽으로 진행한다.
      1. C[j]를 cover 한다.
   3. k + 1 에 대해 탐색을 재귀적으로 실행한다.
   4. r에 O[k] 값을 대입하고, c에 C[r] 값을 대입한다.
   5. j = L[R]에 대해 j  == r 이 될 때까지 왼쪽으로 진행한다.
      1. C[j]를 uncover 한다.
5. c를 uncover 한다.

위와 같은 방식으로 정리할 수 있다. 이 과정에서는 아래로 내려가며, r을 순차적으로 돌면서 각각의 경우에 대해 겹치는 제약조건들을 cover 하였다. 이는 row 하나를 선택했을 때, 깊이 우선적으로 탐색을 진행하면서 backtracking을 하기위한 것으로 위에서 row 비 결정론적으로 선택한다는 표현의 이유이다.

3. 결론

X 알고리즘은 Dancing link 방식을 사용하여 실제로 0-1행렬을 통해 Back tracking을 진행하여 다른 알고리즘에 비해 더 빠른 속도의 Backtracking을 가능하게 하는 방식이다. 하지만, 이러한 방식은 결국 제약 조건이 너무 많아지면 메모리 상의 공간을 상당히 많이 차지하게 되어 너무 많은 경우의 제약 조건에 대해서는 제대로 탐색을 진행할 수 없다는 단점이 존재한다.(전형적인 Time-Space Tradeoff)하지만, 수많은 가능성 중 제약 조건을 모두 만족하는 결과를 빠른 시간 안에 도출해낼 수 있다는 것만으로도 충분히 활용될 여지가 있다고 생각되며, 메모리의 공간 증가보다 프로세서의 속도 향상이 더딘 현재에 있어서는 보다 더 효율적인 알고리즘이 아닌가 생각된다.

 

exact cover 문제 중 하나인 스도쿠를 해결하는 코드는 다음과 같다.

#include <iostream>
#include <sstream>
#include <vector>

#define success 1
#define failed 0


typedef struct name {
    int x = 0;
    int y = 0;
    int value = 0;
}Name;

typedef struct header {
    Name name;
    int size = 0;
    struct header *up = nullptr;
    struct header *down = nullptr;
    struct header *left = nullptr;
    struct header *right = nullptr;
    struct header *column = nullptr;

}Header;

Header* AddHeader(Header* column, Header* current, int x, int y, int value){
    Header *ret = new Header;
    ret->column = column;
    ret->up = column->up;
    ret->down = column;
    ret->up->down = ret;
    column->up = ret;

    ret->name.x = x;
    ret->name.y = y;
    ret->name.value = value;
    if (current == nullptr){
        ret->left = ret;
        ret->right = ret;
    } else{
        ret->left = current;
        ret->right = current->right;
        current->right = ret;
        ret->right->left = ret;
    }
    column->size++;
    return ret;
}

Header* ConstructDancingLink(int data[9][9]){
    Header *master = new Header;

    master->left = master;
    master->right = master;
    Header *current = master;
    for (int i = 0; i < 81; i++){
        for (int j = 0; j < 4; j++){

            current->right = new Header;
            current->right->left = current;
            master->left = current->right;
            current->right->right = master;

            current = current->right;
            current->column = current;

            current->up = current;
            current->down = current;
            current->column = current;

            int div = i / 9, mod = i % 9;
            switch(j){
                case 0: //value exist in board
                    current->name.x = mod;
                    current->name.y = div;
                    break;
                case 1: //row contains certain value
                    current->name.x = div;
                    current->name.value = mod + 1;
                    break;
                case 2: //column contains certain value
                    current->name.y = div;
                    current->name.value = mod + 1;
                    break;
                case 3: //block contains certain value
                    current->name.x = div;
                    current->name.value = mod + 1;
            }
        }
    }
    for (int i = 0; i < 81; i++){
        int x = i % 9, y = i / 9;
        if(data[y][x] > 0){
            current = nullptr;
            Header* column = master;
            for(int k = 0; k < 324; k++){
                column = column->right;
                switch(k % 4){
                    case 0: //value exist in board
                        if (column->name.x == x && column->name.y == y){
                            current = AddHeader(column, current, x, y, data[y][x]);
                        }
                        break;
                    case 1: //row contains certain value
                        if (column->name.x == x && column->name.value == data[y][x]){
                            current = AddHeader(column, current, x, y, data[y][x]);
                        }
                        break;
                    case 2: //column contains certain value
                        if (column->name.y == y && column->name.value == data[y][x]){
                            current = AddHeader(column, current, x, y, data[y][x]);
                        }
                        break;
                    case 3: //block contains certain value
                        int blockX = x / 3, blockY = y / 3;
                        if (column->name.x == blockY * 3 + blockX && column->name.value == data[y][x]){
                            current = AddHeader(column, current, x, y, data[y][x]);
                        }
                }
            }
        } else{
            for (int j = 0; j < 9; j++){
                current = nullptr;
                Header* column = master;
                for(int k = 0; k < 324; k++){
                    column = column->right;
                    switch(k % 4){
                        case 0: //value exist in board
                            if (column->name.x == x && column->name.y == y){
                                current = AddHeader(column, current, x, y, j + 1);
                            }
                            break;
                        case 1: //row contains certain value
                            if (column->name.x == x && column->name.value == j + 1){
                                current = AddHeader(column, current, x, y, j + 1);
                            }
                            break;
                        case 2: //column contains certain value
                            if (column->name.y == y && column->name.value == j + 1){
                                current = AddHeader(column, current, x, y, j + 1);
                            }
                            break;
                        case 3: //block contains certain value
                            int blockX = x / 3, blockY = y / 3;
                            if (column->name.x == blockY * 3 + blockX && column->name.value == j + 1){
                                current = AddHeader(column, current, x, y, j + 1);
                            }
                    }
                }
            }
        }
    }
    return master;
}
void Cover(Header *column){
    column->left->right = column->right;
    column->right->left = column->left;

    for (Header *row = column->down; row != column; row = row->down){
        for(Header *current = row->right; current != row; current = current->right){
            current->up->down = current->down;
            current->down->up = current->up;
            current->column->size--;
        }
    }
}
void UnCover(Header *column) {
    column->left->right = column;
    column->right->left = column;
    for(Header *row = column->up; row != column; row = row->up){
        for(Header *current = row->left; current != row; current = current->left){
            current->up->down = current;
            current->down->up = current;
            current->column->size++;
        }
    }
}

int Search(Header *master, int depth, std::vector<Header *> &solution){
    if (master->right == master){
        return success;
    }

    // set start column for search efficiency
    Header *current;
    int size = INT32_MAX;
    for (Header *column = master->right; column != master; column = column->right){
        if (column->size < size){
            current = column;
            size = column->size;
        }else if(column->size == 0){
            return failed;
        }
    }
    Cover(current);
    for (Header *next = current->down; next != current; next = next->down){
        solution.push_back(next);
        for (Header *row = next->right; row != next; row = row->right){
            Cover(row->column);
        }
        //to find a one exact cover, if you need to find multiple exact cover remove this branch
        if (Search(master, depth + 1, solution) == 1){
            return success;
        }else {
            solution.pop_back();
            for (Header *row = next->left; row != next; row = row->left){
                UnCover(row->column);
            }
        }
    }
    UnCover(current);
    return failed;
}


void Clear(Header *master) {
    for(Header *column = master-> right; column != master; column = column->right){
        Header* tmp;
        for (Header *row = column->down; row != column; ){
            tmp = row->down;
            free(row);
            row = tmp;
        }
        tmp = column-> right;
        free(column);
        column = tmp;
    }
    free(master);
}
int main() {
    std::cin.tie(0);
    std::ios_base::sync_with_stdio(0);

    int data[9][9];
    for(auto & i : data) {
        std::string input;
        getline(std::cin,input);
        std::istringstream splitted(input);
        for (int & j : i){
            splitted >> j;
        }
    }

    std::vector<Header*> solution;
    Header *master = ConstructDancingLink(data);
    Search(master, 0, solution);
    for (auto& i : solution){
        data[i->name.y][i->name.x] = i->name.value;
    }
    std::ostringstream result;
    for(auto & i : data) {
        for (int j = 0; j < 8; j++) {
            result << i[j] << " ";
        }
        result << i[8];
        result << '\n';
    }
    std::cout << result.str();
    Clear(master);
    return 0;
}